Letter is what we call the smallest semantically independent unit of alphabetic writing. †Diacritical marks in themselves do not carry meaning, but are added to letters to modify the latter’s value. Though they are part of the meta writing system in which alphabetic writing is embedded, punctuation marks do not belong to the alphabet either, and neither do numerals and various ‘letterlike’ symbols and miscellaneous sorts.Letters carry meaning, usually phonetic: they represent sound. Letters are the conceptual glue between speech and writing. Speech is spoken language and thus can be heard; writing is graphic language and therefore inaudible. Letters, being symbols, referring from one order to the other, are both at once: they can be seen as well as they can be heard. They are made visible through written figures which we call graphemes. They are made audible through speakable names. Letters may have many names, depending on the language that calls them; they may change position in the order in which languages recite them. Languages are said to have different alphabets, composed of different letters, with different names, and arranged in different orders. There is however only a single Alphabet, which is the set of all letters. And it will appear that that set may turn out very small, but with many ways of looking at it, of sorting, arranging and collating. There are even more aliases for its elements, the letters. Graphemics is the study of these aliases and its subject are graphemes and the mutual relationships that connect them. These deserve a foundational theory to be further developed.
The diagram in Figure 1 shows the family tree of the Phoenician letter Zayin. In the order of the Greek alphabet (where it takes the same position †Seventh if you count in, as it should, Wāw ⟨𐤅⟩, also known, in Greek, as Digamma ⟨Ϝ⟩, or, in Latin, as Ef.as it does in the Phoenician abjad) it is known as Zeta. In the Latin abecedary (where most locales usually put it last) we just call it Zæt, Ze, Zet, Zett, Zède, Zo, or (if you speak Italian or Spanish) Zeta again. In the Cyrillic azbyka of Slavonic languages, it may be called Dzělo, Zemlja, Živěte †Actually ⟨Ж ж⟩ derives from the Glagolitic ⟨Ⰶ ⰶ⟩, of whose origins paleography is still in the dark. While it has been proposed that it may have been made up from doubling and mirroring the Hebrew letter Shin ⟨ש⟩, I’d conjecture it may perhaps be demonstrated to have derived from ⟨Z⟩ after all. But doing so will require a more thorough working-out of the graphemic model I here introduce, and of the transformative operations that will allow us to explain how graphemes can mutate and evolve from one representation of a letter into another, and in the process create ‘new’ letters. Dze, Ze, Zje, depending on its phonetic usage and graphemic appearance. Armenian, Kartvelian, and Aghuanic languages perform(ed) an even greater variety in strident and sibilant consonants than are distinguished by the Slavonic tongue. Consequently, the Caucasian alphabet(s) †I am treading on thin ice now. Scholarly consensus of course rejects the attribution to St Mesrop Mashtots as the sole creator of Caucasian scripts. One shall indeed agree that – at least before the nineteenth century – alphabets simply are very unlikely to be contrived by a single inventor, but instead evolve naturally from scribal variety in local hands or derailing calligraphic mannerism, eventually divaricating into separate ‘alphabets’. The orginis of the Armenian script remain an unsolved mystery, but the open-minded reader must recognize the evident similarities between ⟨Զ⟩, ⟨Ձ⟩, ⟨Չ⟩, ⟨Ջ⟩, and with some good will may also approve of the comparison between ⟨Ծ⟩ and ⟨Ճ⟩. The origins of Georgian scripts – a single alphabet, I would dare to propose, as it will appear once graphemic theory can be rigorously applied – is especially problematic. It would make for a great case study, having graphemics prove its worth. In the pedigree of Zeni one can already see the graphemic lineage ⟨Ⴆ⟩ → ⟨ⴆ⟩ → ⟨ზ⟩ that connects Asomtavruli and Nuskhuri with Mkhedruli. It’s therefore all the more unfortunate that Unicode has done again (v11.0) what paleographic history keeps pointing out should not be done: to compartmentalize and canonize transient contingencies from a dynamic continuum always in flux, thereby making up ‘new’ alphabets out of thin air, and adding to the disarray of letter conflations, which in the case of Georgian is a single alphabet that was the victim of graphemic illiteracy and overzealous trivision already.with which these are written must also display great variation to adequately represent the sounds of Z, with surrogate letters called Za, Ze, Ça, Ja, Č̣ē, Ša, Ča, J̌ē, C’ò (Armenian), Zeni, Zhani, Dzili, Jani (Georgian), Zarl, Zhil, Cha, Sha, Car, Chi, Cyay, Shak, Jayn, Dzay, Chat, Seyk (Caucasian Albanian). Though it may change position in the collation order (and consequently acquire different numerical value), and even though it multiplies and masquerades in many costumes, Zayin/Zeta/Zet/Dzelo/Za consistently represents the same phonemic value space (taking into account phonetic shift): [dj, dz, dzʲ, dʒ, d͡z, s, st, sʲ, tʲ, t͡s, tsʰ, tʃ, tʃʰ, θ, zd, zʲ, z(ː), z̠, ð, ʃ, ʃt, ʒ] — all the while, it really remains the same letter.
The descent of Greek Zeta from Phoenician Zayin is a well known trivium. But one never reads how the transmission from Zayin’s most commonly attested glyphic figure in epigraphy, ⌶-beam ⟨𐤆⟩, to the canonical grapheme for Zeta, zigzag ⟨Z⟩, is to be understood exactly. It seems intuitively obvious. †Especially when such intuition is instructed by even the slightest bit of practical experience with handwriting. (Just try to write ⟨⌶⟩, i.e. with a single, uninterrupted stroke, never tracing the same path twice, and not lifting the tip of your pen until the shape is done.) Note that in the earliest history of writing it may very well have been the other way around with the cursive form ⟨�⟩ predating the formalized ⟨𐤆⟩. Chronology matters in paleography; in graphemics not so much. If we can define a function which maps ⟨⌶⟩ to ⟨⥍⟩, then we can also define one vice versa, which maps ⟨⥍⟩ to ⟨⌶⟩, and, if necessary, update the graphemic genogram accordingly, without much impact.Mathematically, however, it is not. The state of the art, sadly, is that letter descent is generally described informally, with haphazard metaphorical iconography, leaving too much room still for ambiguity and Hineininterpretierung. We lack the methodology to formally formulate the precise shape of graphemes, and to rigorously demonstrate graphemic descent. This is why paleography is rife with tenuous speculation about the origin of letters. Historians look at material ‘witnesses’ to corroborate hypothesis by empirical induction. (They rely on a statistical conception of Truth, as do type designers who seek refuge with user tests to obtain scientific proof for the correct drawing of their glyphs.) In graphemics we instead should attempt to deduce proof from first principles. (In the platonic universum of mathematics, unfettered by chronology or utilitarian fitness as we are, we can study shape instead of symbol.) These graphemic principles are to be found in the orbital mechanics and motorics of writing (ductus) and in the underlying topology of letters (construction). (Proportion and geometry are important only to calligraphy and type design.)
Figure 2 — Often minuscula have evolved from capital letters: both are scribal variations of the same letter. Forgetful of this graphemic fact, orthography artificially invented the bicameral alphabet, divorcing uppercase and lowercase letters. Paleography did not want to stay behind and so came up with the anachronism of ‘majuscules’ (an etymological oxymoron). But history is recalcitrant and more than once evolution goes against grammatici’s direction when ‘capitals’ suddenly arise from ‘rounds’. There is a graphemic category difference, though: capitals belong to formal, monumental writing; minuscules are the product of informal, chancery shorthand. The latter is cursive script and exaggerates the ductus of letters (in extremis with a single continuous stroke). The former is interrupted or ‘fraktur’ script, and shows letters’ construction more than it reveals their ductus. In both cases, however, the underlying topology is the same. Until it isn’t: and that is when we finally may have to admit that a new letter is born. — The de facto canonical graphemes for the Greek lowercase letters are cursive; in the case of Alpha, ⟨Α⟩ and ⟨α⟩ are still homotopy equivalent. In the case of Zeta, ⟨Ζ⟩ and ⟨ζ⟩ are not, depending on how express you’d write or design the loop at the top-right retraction, or, mutatis mutandis, how ‘fuzzy’ homotopy considers the outlines of the resulting graphic.
The graph in our diagram in Figure 1 is (almost) hierarchical: in the data structure nomenclature of information theory a ‘tree’ indeed. But this shouldn’t confuse us, because letters may evolve from one parent (mutation), but also can be begotten as the bastard of two or even three or more ancestors (evolution and analogy). Unlike is the case in genetics, where (most) species of living organisms reproduce through a function of addition of two parents (sex), letters spring off either through an operation on two or more operands (averaging or otherwise combining the feature sets of ≥2 parental graphemes), or as the product of a single ancestor and some function of graphemic transformation.
Each glyph on our tree is a node in the graphemic graph. Glyphs in dashed boxes are hypothetical conjectures. †These graphemic conjectures may very well appear to be paleographically attested, but that would only redundantly prove us right. Although a lineage of graphemic transformations may turn out to also be a paleographic pedigree (ideally, both coincide), this is not always the case here. Here we only are concerned with transformation of shape, not (yet) with evolution or historically provable descent. It’s charming, for example, to see that the script uppercase ⟨𝒵 ⟩ (an invention of sixteenth and seventeenth century Dutch and English penmasters) resolves to the exact same grapheme with which it all started (though a cross stroke had to be added to ⟨𝒵 ⟩ in order to better disambiguate it from ⟨𝒯 ⟩).Those in solid boxes are representative glyphs for characters which are encoded in Unicode’s Universal Character Set. The arrows between the nodes show the vertices (edges, pairwise relationships) of our graph. Each node is the product of one or more ancestral graphemes and some graphemic operation implied in the vertex that connects them. The graphemic genogram is a directed graph: the operation implied in the vertex is not reversible. For example, applying an operation of cursive ‘smoothing’—i.e. increasing the ductus velocity (speed of writing)—on ⟨Z⟩ will yield ⟨շ⟩ or ⟨2⟩, but re-applying that same operation on ⟨շ|2⟩ will produce ⟨Ꙅ⟩. It is conceivable though to apply the inverse function (i.c. formalization via interrupted construction or ‘sharpening’) on the product ⟨Ꙅ⟩ to again obtain the input graphemes ⟨շ|2⟩ and ⟨Z⟩. But while distinctive topological information may get lost in transformation, the derivative of the inverse transformation may consist of multiple possible alternatives. This is notably the case with homographs, which are characters represented by the same grapheme, but of different graphemic descent.

Figure 3 — Cyrillic Ze ⟨З⟩ and ‘Latin’ Ezh ⟨Ʒ⟩ are two graphemic variations on the same meta letter Zeta: they have different pedigrees, acquired different phonetic value in different linguistic contexts, but at long last originate from a common ancestor ⟨Ζ⟩. As far as pure graphemics is concerned, Abkhasian Dze is identical to Ezh, while they are represented by the exact same grapheme ⟨Ʒ⟩. Historically, though, it could be argued they are homographic only, because the latter was made in the image of Gothic cursive’s ‘tailed’ Z ⟨𝔷⟩, while the former was (probably) modified from Ze. In both cases the confusion is due to the invention, in the nineteenth century, by separate subfields of linguistics, unaware of each other’s coinciding fabrications. In the natural flow of paleography though, such concurrences happen rarely. But if they do, we have true cases of homography, when unrelated symbols with completely different semantic value and of alien graphemic origin arrive at the same graphemic figure through distinct lineages, as is the case with the more usual form of the Latin numeral three ⟨3⟩ and Cyrillic Ze ⟨З⟩, on the one hand, and with Ezh/Dze ⟨Ʒ⟩ and a stylistic ‘flat top’ alternative for three ⟨�⟩, on the other. Likely, symbols which are used to represent numerical values only are more resilient against semantic shift: integers are by definition discrete, and (barring the constants of mathematics and physics) we do not assign dedicated symbols to non-integer scalars, for then we would literally end up with an infinitesimal number in the repertoire (which, after all, still needs to fit into the memory capacity of a literate human being). Letters’ values, on the other hand, do shift, and alphabets consequently need to recycle allographs as much as possible, repurpose them as symbols with slightly or considerably different meaning, and so upgrade them to character status.
If you recall Gerrit Noordzij’s The Stroke, theory of writing, Figure 4 might feel familiar. It may anyway reveal what I here only briefly – and at once all too abstrusely – try to explain: graphemic space is a manifold continuum where infinite instances exist along multiple axes of transformation. (The dimensions shown in Figure 4 are anything but exhaustive, even for the simple case of ⟨Z⟩. Many more axes of graphemic transformation can be added – but that would spoil the visual’s didactic merit.) Instead of interpolating the outlines of glyphs, we are now exploring mutations of grapheme topology and ductus. The resultant forces which operate the ductus and cause topology changes, could be defined as simple functions. At least, that’s the postulation we’d like to see approved.
| (A ∨ E) + ◌̄ = � | (union; addition) |
| 𝑘(◻, ⬦) = ○ | interpolation or blending |
| 𝑔∘𝑓(Z) = ç | composition of two graphemic morphisms |
| 𝑓: Z → ꝣ | graphemic operations yet to be defined |
| 𝑔: ꝣ → ç |
In mathematics the graphemic functions which we have in mind, might be called morphisms. They are to graphemes as what in linguistic morphology alternations are to morphemes (like the suffixes of plural markers), or as what in phonology sound changes are to phonemes (like vowel shifts). We can easily imagine graphemic pendants to the phonetic concepts of assimilation, dissimilation, elision, epenthesis, fortition, lenition, metathesis, nasalization, palatalization, etc. But unlike the anatomical metaphors of linguistic method, we’d better exploit the graphic nature of graphemes and aim to express them formally so we can compute their relationships.
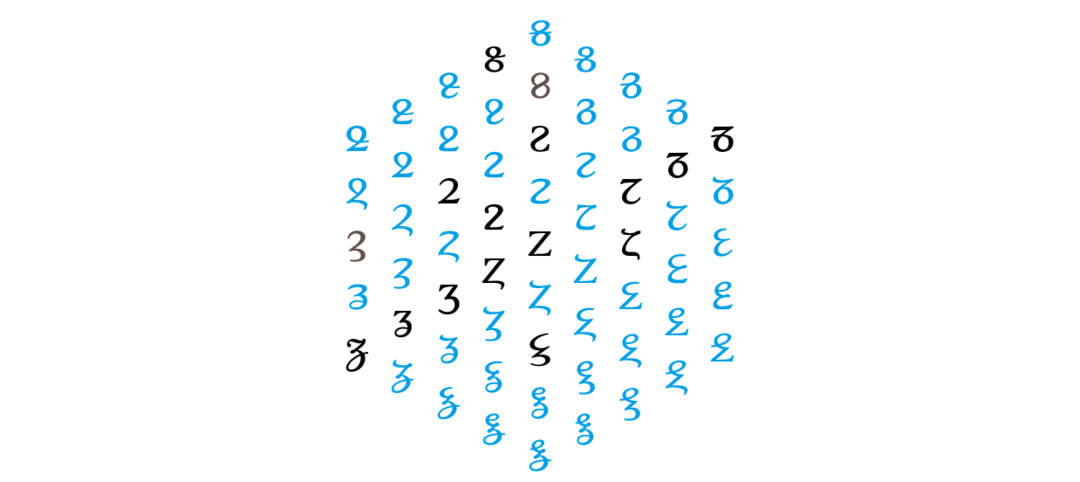
Figure 4 — An (incomplete) periodic view on the grapheme space for ⟨Z⟩. Solid glyphs represent existing characters (i.e. encoded in Unicode); sketched glyphs are theoretical graphemes, which may lead to the discovery of new letters, or help to understand the origins of those we know already but take for granted. Just imagine how in the paleographic history of a parallel universum the bottom graphemes would have given rise to a character ⟨S̷⟩.
Drawing glyphs is laborious. Type designers know it’s hard to make a living from their efforts, which are even less rewarding when it concerns conjectural graphemes, that more than likely will remain but single-purpose disposables. Moreover, much of the reasoning about the underlying graphemic construction of glyphs goes unnoticed, because it hides in an incomprehensible array of (𝑥,𝑦) coordinates, instead of a formally falsifiable, coordinateless data structure which abstracts proportion and modulation. Imagine we could conveniently notate graphemic properties, in algebraic form that is, instead of having to draw glyphs. Say we were to revive the ideal of parametric fonts in a way that went beyond variations in contrast, weight and the modeling of serifs and terminals. Suppose graphematicians could gratuitously jot down graphemes at will and discuss their properties unambiguously. Modulation (translation, expansion, rotation) is well understood, and implementations that mimick the behavior of the broad nib pen are again finding their way into current type design software. What is missing though, is a proper understanding of ductus and construction, and of the constraints that govern writing. Most importantly, it is the want of a solid mathematical foundation that leaves graphemics a discipline we still have to invent anew. I am looking forward to further contribute towards that goal and hope to have put forward at least a few ideas to stimulate attention.
Meanwhile, here is an exercise for mathematicians. Can we (a) formally express the characteristic features of graphemes as uniquely identifiable topologies such that (b) we can define functors which explain the transformation from one graphemic instance into another, thereby discretely classifying graphemic instances into grapheme categories (and thus defining precisely what is a grapheme and what it is not)? Or put differently: are we able to come up with a formal descriptor and data structure to adequately capture the underlying model for the category of all graphemic objects which represent all paleographic attestations of, for example, ⟨𝓏⟩, all its artistic manifestations in typeface design, and all the many ways people may (still legibly) write lowercase z? Next, can we then also map that category ⟨𝓏⟩ to a category ⟨𝔷⟩, ⟨𝔷⟩ to ⟨ʒ⟩, ⟨ʒ⟩ to ⟨Z⟩, and finally ⟨Z⟩ to ⟨𐤆⟩?
And here a challenge for computer programmers. Once a solid mathematical foundation of graphemic topology will have been established, then, given the set of graphemes ⟨Z, ʒ, ꝣ, ç⟩, can we programmatically infer the genogram which most probably relates ⟨ç⟩ to ⟨Z⟩? †Though most other genetic relationships shown in Figure 1 are my conjectures, C-cedilla’s ⟨ç⟩ descent from Z, via Visigothic Z ⟨ꝣ⟩ is an established fact of paleography, and a nice trivium to market graphemics as a field of study whose further exploration we can only hope may in our lifetime become acknowledged as a profession, else get endowment outside of academia.And still: given a digital font, for each glyph, can we trace its centerline and convert the bézier coordinates into a generalized coordinateless topological grapheme encoding, next, having computed the delta to all other glyphs, cluster them by similarity, perhaps even test for degrees of homography?
And finally, a consideration for character encoding experts and Unicode spec writers. Suppose a solid mathematical model for graphemic identifiers would become available, along with an elegant formal and computable notation, and suppose we were able to programmatically generate glyphs from such codified description, would it then be thinkable to employ that as a normative character property, perhaps in place of the informative reference glyphs which more than once have shown to be adding more to the conflation of graphemes and letters (characters) than that they help to illustrate what some letter should look like in order to be rightfully called by that letter’s name?
Leuven, June–July 2018